滾動中的物體

前面的幾個章節裡，我們探討了轉動中的物體，並且計算了 轉動慣量和轉動動能。在這個章節裡，我們將要分析一個比較有趣、特殊，卻在生活中常常遇見的情形—滾動。

滾動 = 轉動 + 平移

在尚未學習轉動動能之前，假設你想要計算一顆輪胎在地上滾動時所具有的動能，你可能會以其質心速度與 $\frac{1}{2}mv^2$ 的公式計算它的平移動能；在學習了轉動動能後，你可能會想要以其質心的角速度與 $\frac{1}{2}I\omega^2$ 的公式計算它的轉動動能。那麼究竟哪一個才是對的呢？其實，這兩種算法都只對了一半。

就以上面的例子來看，一顆滾動中的輪胎，可以被想像成一個正在平移的質點，因此其具有平移動能；它也可以被看成一個繞著中心轉動的物體，因此其具有轉動動能。也就是說，在計算它的滾動動能時，我們要計算的不是 $\frac{1}{2}mv^2$，也不是 $\frac{1}{2}I\omega^2$，而是兩者相加後的結果。

於是我們知道，在分析一個滾動中的物體時，可以將其運動拆解為純平移和純轉動，如下圖所示：

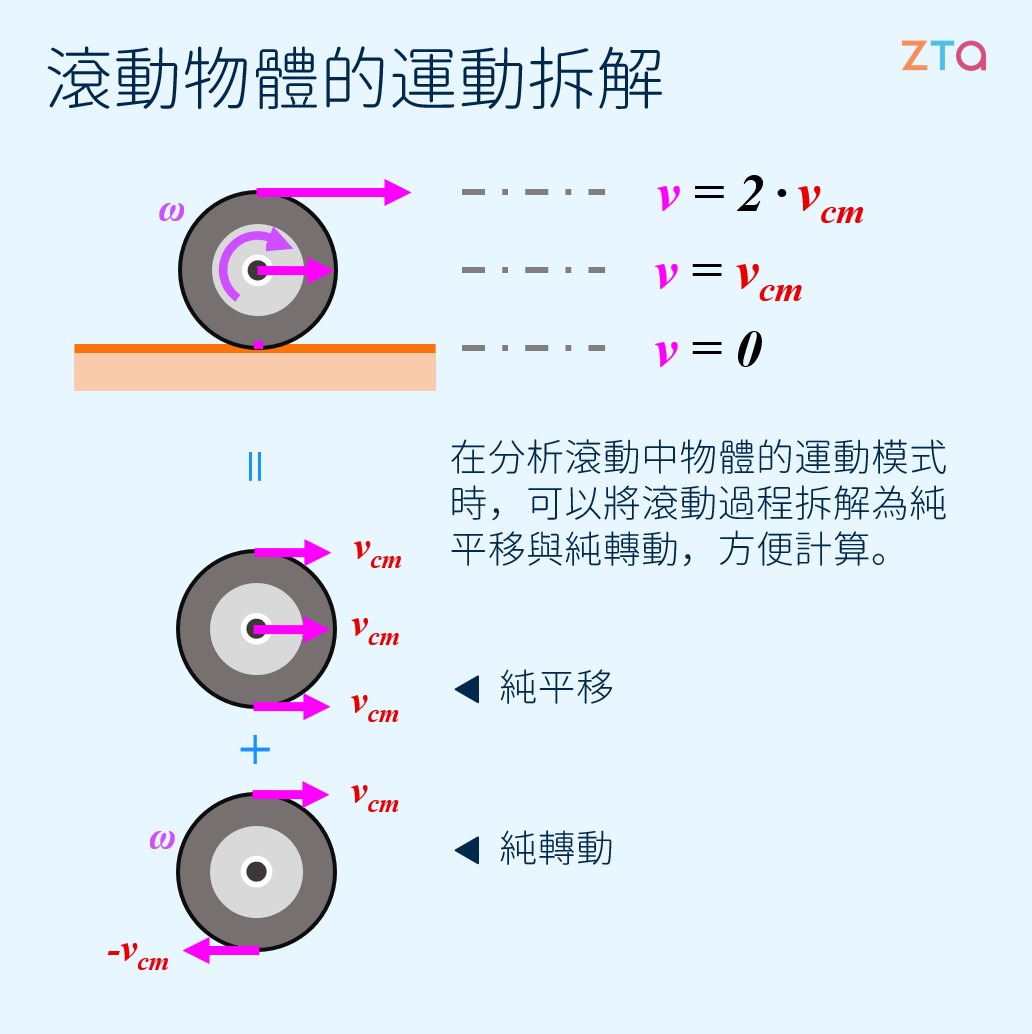
值得注意的一點是，滾動中的輪胎與地面接觸的那一點，速度是 0；輪胎中心速度等於其質心速度，而輪胎頂部的速度等於兩倍的質心速度。

滾動動能

如同上面所說的，我們可以將物體的滾動拆解成純平移和純轉動。因此在計算物體滾動時所具有的動能時，我們可以將其平移動能與轉動動能相加。其中，$I$ 是物體質心的轉動慣量，$\omega$ 是物體的角速度，$m$ 是物體的質量，$v$ 是物體的質心速度：

$E_k = E_v+E_\omega$

$=\frac{1}{2}I\omega^2+\frac{1}{2}mv^2$

接觸點的摩擦力

如果一顆輪胎在地上等速度滾動，則其除了輪胎上各點本身的向心加速度外，並沒有任何的加速度。在這樣的情況下，輪胎與地面間不存在任何摩擦力。的確，在等速度的情況下，加速度 $a$ 等於 0，則根據 牛頓第二定律 ，受力 $F = ma$ 也會等於 0。

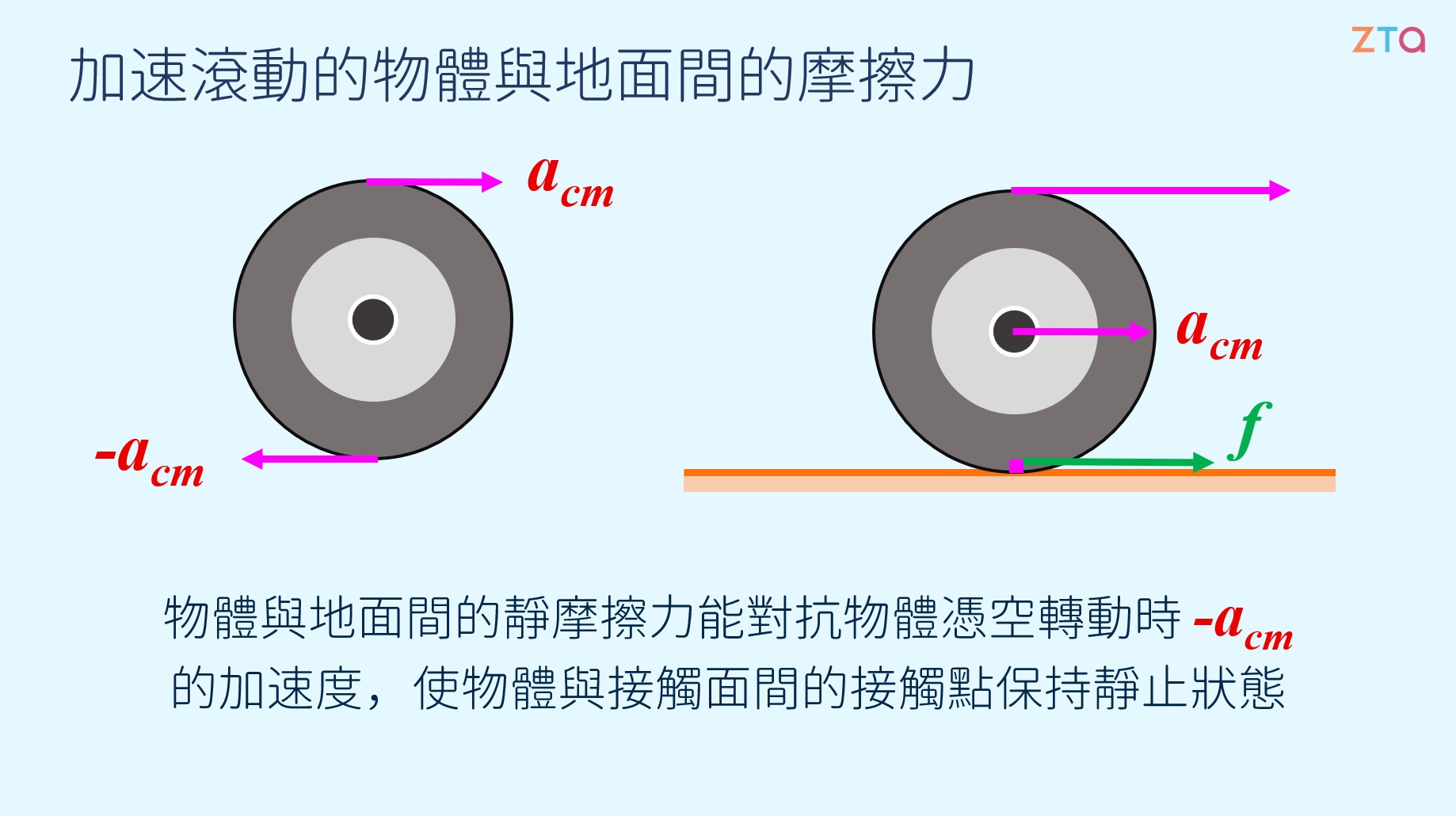
然而，如果輪胎開始加速或減速，就代表摩擦力不再是 0 了。讓我們想像一顆靜止的輪胎，此時，某些原因使其開始向前轉動。倘若其與地面間沒有摩擦力，則輪胎只會在原地旋轉，而不會向前滾動。

但是因為接觸面兼具有 摩擦力，使得輪胎與地面間沒有滑動的狀況出現，才讓輪胎有向前滾動的趨勢，如同圖中所示：

沿著斜面滾動

在探討完水平面上的滾動後，是時候來討論滾下斜面的物體了。讓我們假設一顆半徑 $R$ 、質量 $M$ 的輪胎滾下一個角度 $\theta$ 的斜坡。此時，輪胎只受了三個力：重力 $Mg$、斜坡的正向力 $N$、斜坡的靜摩擦力 $f_s$。如圖所示：

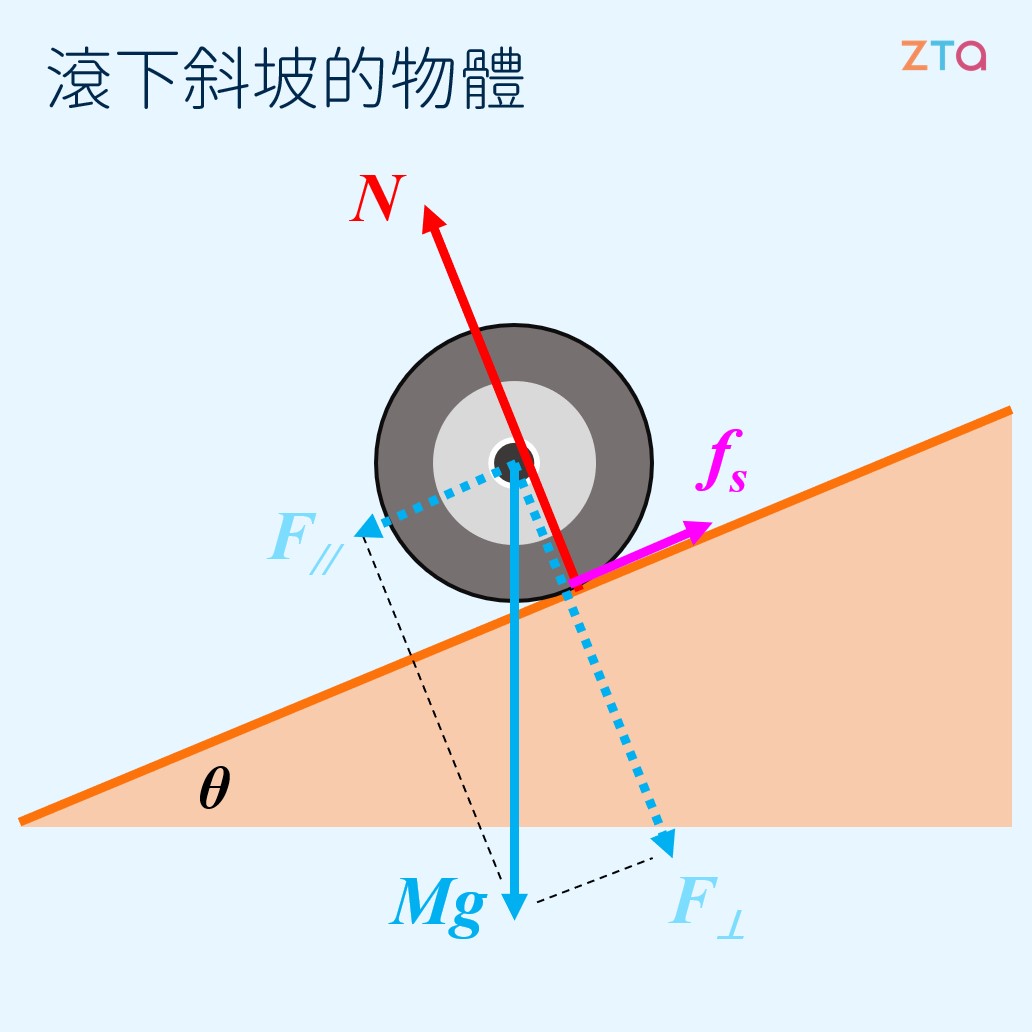
我們將往斜坡上方的方向定為正，因此，輪子滾下斜坡時的加速度 $a_{cm}$ 應該為負。接著，因為正向力已經把重力垂直於斜面的分力抵銷掉了，因此在分析力時，我們只需要關注平行於斜面的力。如此，我們便能寫出力與加速度間的關係式：

$Ma_{cm} = f_s - Mg\cdot sin(\theta)$

接著，我們將目光放到輪胎與斜面的接觸點上。摩擦力在這點上對輪胎的中心作用了一個力矩，這個力矩使得輪胎沿著自己中心旋轉。接著，因為力矩等於垂直的力臂（此處即為半徑）乘以力，我們能寫下：

$Rf_s = I_{cm}\alpha$

其中，$\alpha$ 即為輪胎繞著中心旋轉的 角加速度 。現在，我們有列出了兩個方程式，要想辦法將兩者間建立起關係。此處，我們得要回想一下，輪胎滾動時的切線加速度等於半徑乘上角加速度（$a = r\alpha$），將其代入得：

$Rf_s = I_{cm}\frac{-a}{R}$

注意，我們將逆時針旋轉時的角加速度定為正，然而輪胎的加速度為負，因此上述式子中，$a = -R\alpha$。再經過一次移項，便能求出摩擦力 $f_s$：

$f_s = I_{cm}\frac{-a}{R^2}$

接著，我們將 $f_s$ 代入第一個方程式：

$Ma_{cm} = I_{cm}\frac{-a_{cm}}{R^2} - Mg\cdot sin(\theta)$

移項後提出 $a_{cm}$：

$a_{cm}(M+\frac{I_{cm}}{R^2}) = -Mg\cdot sin(\theta)$

再經過一次移項，便能得到輪胎滾下斜坡的加速度：

$a_{cm} = \frac{-Mg\cdot sin(\theta)}{M + I_{cm}/R^2}$

$=\frac{-g\cdot sin(\theta)}{1+I_{cm}/(MR^2)}$