機
器
人
萬有引力

我們都聽過這個故事:「牛頓坐在蘋果樹下休息,有顆蘋果掉下來砸到牛頓,牛頓開始好奇,究竟為什麼蘋果是向下掉,而不是往上飛呢?經果許多思考與推導後,牛頓提出了眾所皆知的萬有引力定律。」
這個故事是真是假,我們不得而知,但此處我們好奇,萬有引力定律到底是什麼呢?它大概就是在說,任意兩個具有質量的質點間,都會有一個相吸的作用力。如果單純用數學式子表達,我們可以寫出:
其中, 為兩個質點間的萬有引力, 為一個常數, 和 分別代表兩個質點的質量,而 是兩個質點間的距離。萬有引力常數 ,在標準單位下等於:
觀察萬有引力定律的式子,我們可以看到,兩質點間的作用力與兩質點的質量呈正比,也就是說,重幾倍,引力就多幾倍。另外,萬有引力與質點間的距離平方成反比,也就是說,距離越來越遠,引力的大小就越弱,直到無窮遠處趨近於零。
重力可以疊加
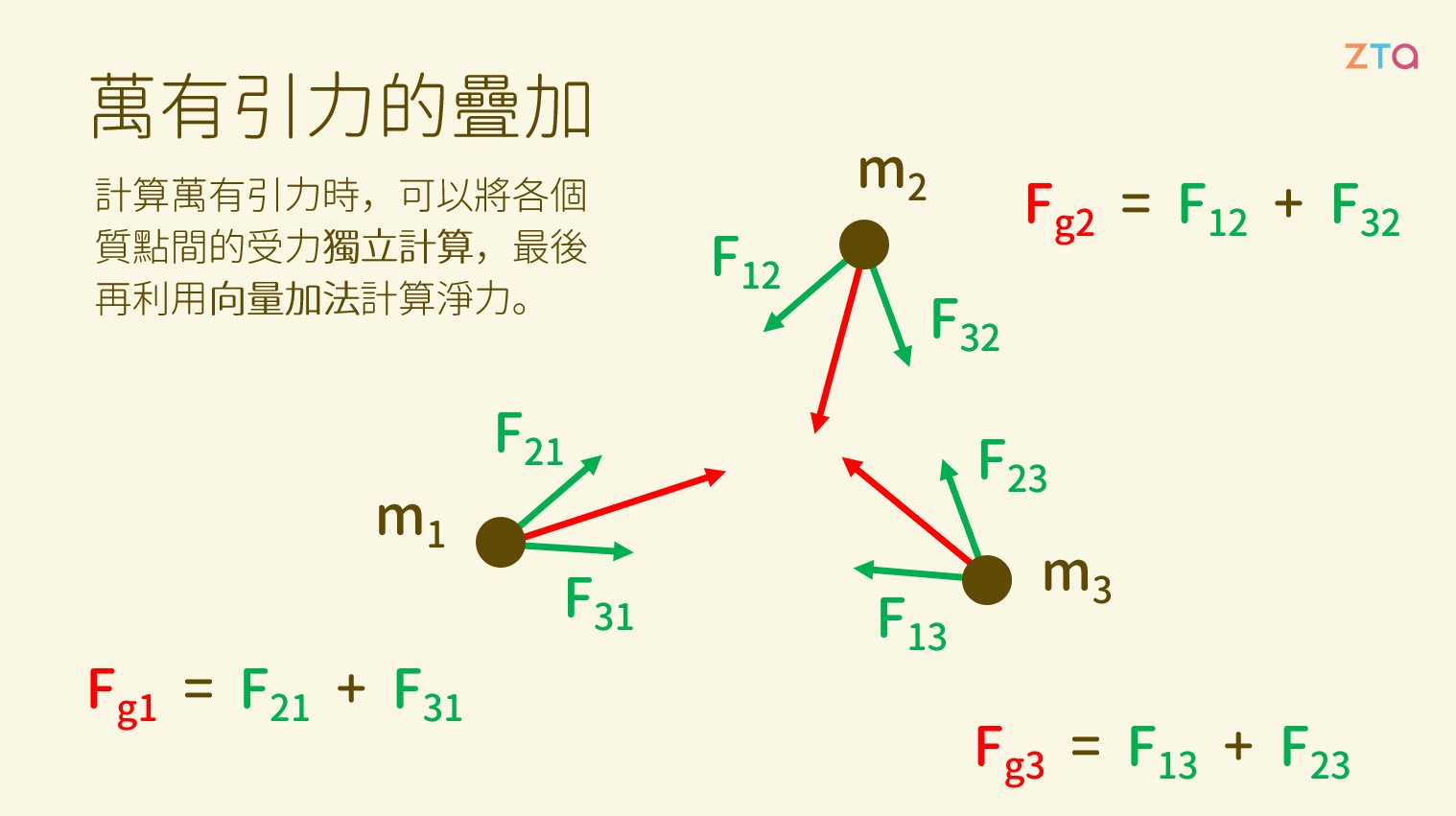
目前為止,我們討論到的都只有兩個質點之間的引力,那麼如果今天有三個質點,我們要怎麼計算它們相互之間的作用力呢?
其實,引力這種東西,本來描述的就是兩個質點間的吸引力而已。在引力的攻式中,質量也只有 和 兩項,因此我們在探討多個質點間的引力時,肯定是需要把各組質點獨立出來看的。
就剛剛所說的三個質點為例,我們可以將各個質點間的受力獨立開來探討,最後再利用向量的加法將質點的總受力合併,如這張圖所說的:
重力加速度
還記的在學習自由落體運動的時候,我們說了重力加速度 嗎?那你曾不曾好奇過,這個數字單純是測量出來的,還是其實它是可以被「算」出來的呢?
答案是:都可以!那究竟要如何計算重力加速度呢?我們可以回想一下牛頓第二運動定律中的 。架設有個質點正在地表附近進行自由落體運動,忽略空氣阻力的話,這個質點所受的力全然是由地球對之的引力提供的,引此我們可以利用萬有引力的公式,結合牛頓第二定律:
將右半部兩側的質點質量 消去,我們可以得:
其中,地球質量 m_地 大約是 ,地表附近與地心距離 大約是 6371000 m,如果把這些我們已經確定知道的數字代入上面加速度的等式,我們就可以得到重力加速度:
均勻球殼的重力
在這裡,讓我們先將思緒跳脫地球。想像一下我們身處在浩瀚宇宙的真空中,四除了一個很薄很薄的球殼之外,什麼東西都沒有。這個球殼的質量為 ,而且質量均勻地分布在球殼的各個部分。
在球殼的內部,有一個質量為 的質點。那麼請問,球殼與該質點間的萬有引力是多少呢?答案很簡單,是 0。為什麼呢?讓我們看看下面這張圖:
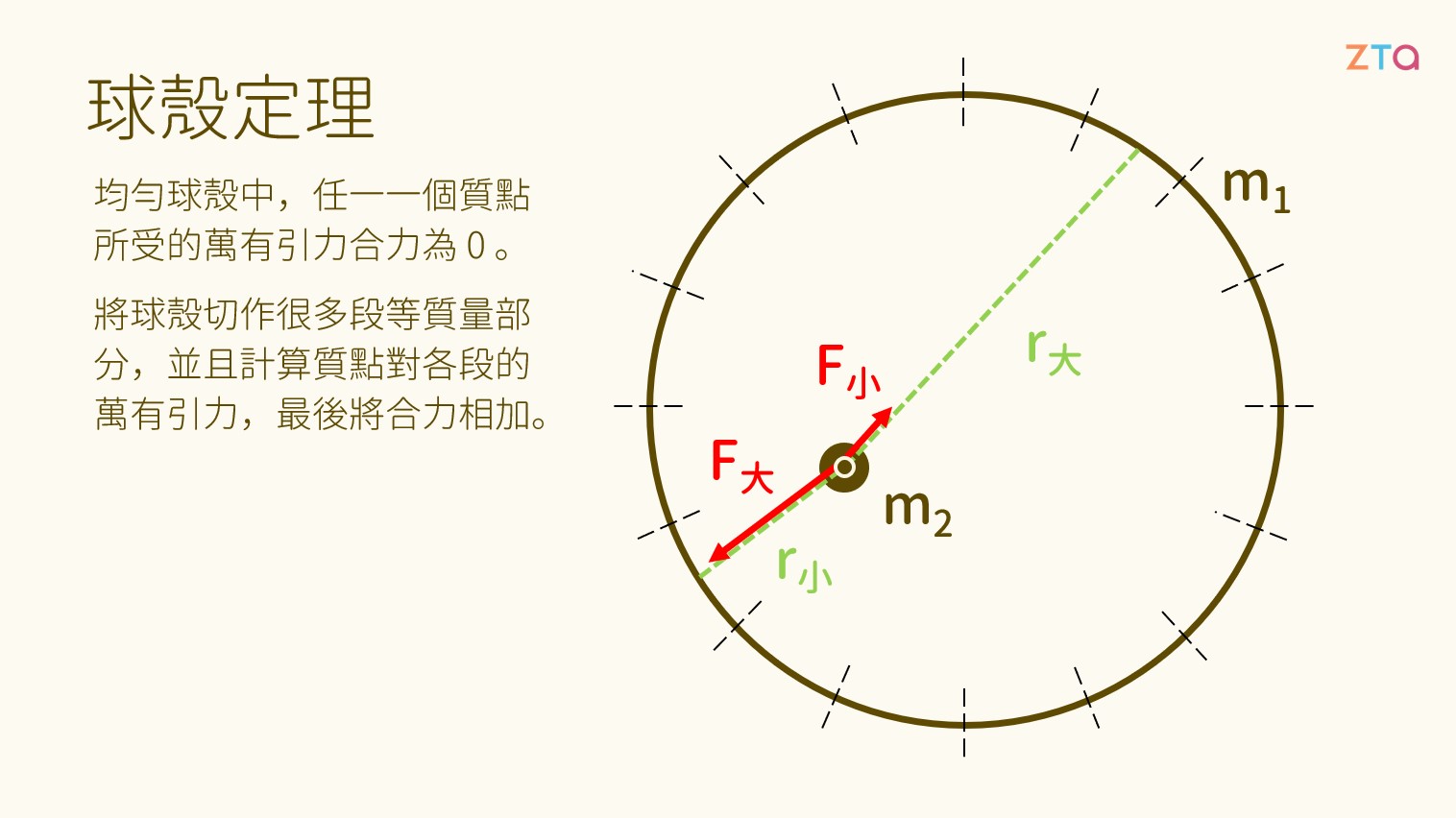
在證明時,我們可以將球殼切作無限多個等質量的小部分,接著計算質點對各個小段間的萬有引力。對於距質點較近的球殼部分而言,因為距離 較小,萬有引力較大;對於距質點較遠的球殼部分而言,距離 較大,萬有引力較小。
然而,距質點較遠的球殼部分,占了整個球殼的較大一個部份,因此儘管各部分的萬有引力較小,將各個部分的引力相加後,對質點造成的引力還是相當可觀個。經過積分計算後,我們會發現球殼對內部任一質點所造成的引力是 0。
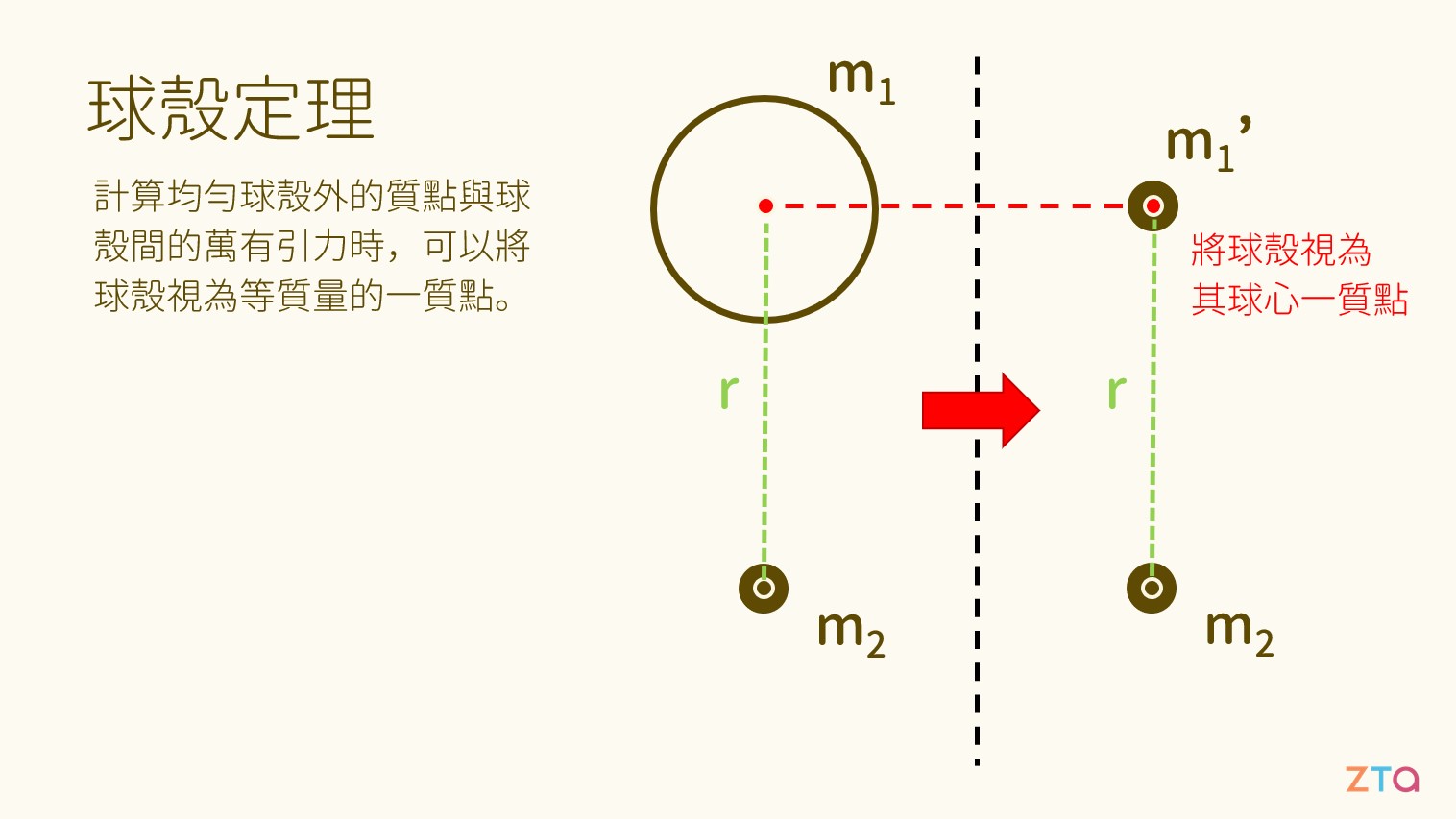
而如果今天要計算球殼對其外部任一質點造成的萬有引力,我們可以將球殼視為位於其質心的一個質點,這麼一來,計算的過程就簡單多了!這同樣可以經過積分證明之。
地面下的重力
在理解完均勻球殼對質點所造成的萬有引力後,我們可以來探究在地平面之下的重力了。目前為止,我們所討論在地球上的重力,都是在描述地表附近的物體受地心引力的影響,但你有沒有想過,如過這個物體不在地表,而是在地底呢?
既然我們已經學習完了球殼,那為什麼不化繁為簡,將地球變成很多個球殼呢?我們暫時將地球假設作一個質量分布均勻的球體,接著把地球分成多個球殼:
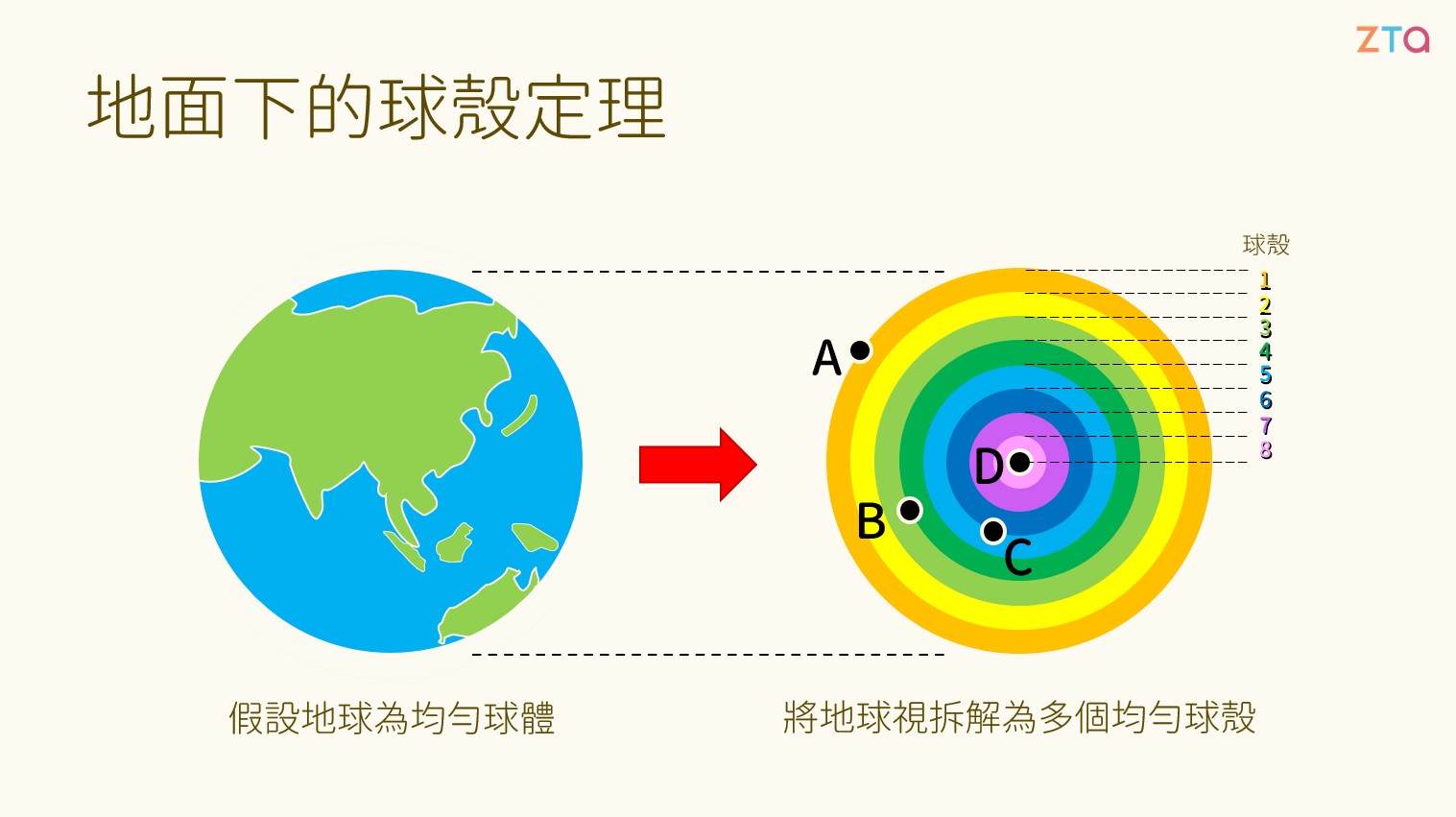
假設現在要計算 B 點所受的萬有引力,我們就可以使用球殼定理。B 點位於球殼 1、2、3 的內部,因此所受到球殼 1、2、3 的萬有引力為 0。接著我們看看,B 點位於球殼 4、5、6、7、8 的外側,因此我們可以將球殼 4、5、6、7、8 合併做位於地心的一個質點。
這麼一來,我們只需要考慮球殼 4、5、6、7、8 所具有的質量,並且帶入萬有引力的公式,就可以求出 B 點所受的重力大小了。在此我們得到一個結論:探討地下質點的重力大小時,只需考慮質點之下的地球。例如現在若要探討 C 點所受的重力,我們只需計算球殼 6、7、8,不須理會其他部分。
利用這個結論,我們可以得到一個地表之下質點通用的重力公式。因為我們假設地球的質量分布均勻,因此任意一點的密度必定相同:
假設地球半徑 ,而質點距離地心 ,將其帶入球體體積公式可得:
利用等量公理求得 :
將其代入萬有引力公式即可得到:
由此我們得知,當質點位於地表之下時,其所受的地心引力是其在地表所受的地心引力乘以當下位置與地球半徑的比例。最後,讓我們把上面得到的結論,與地表之外的萬有引力公式整合在一起,便能得到以下這張圖。
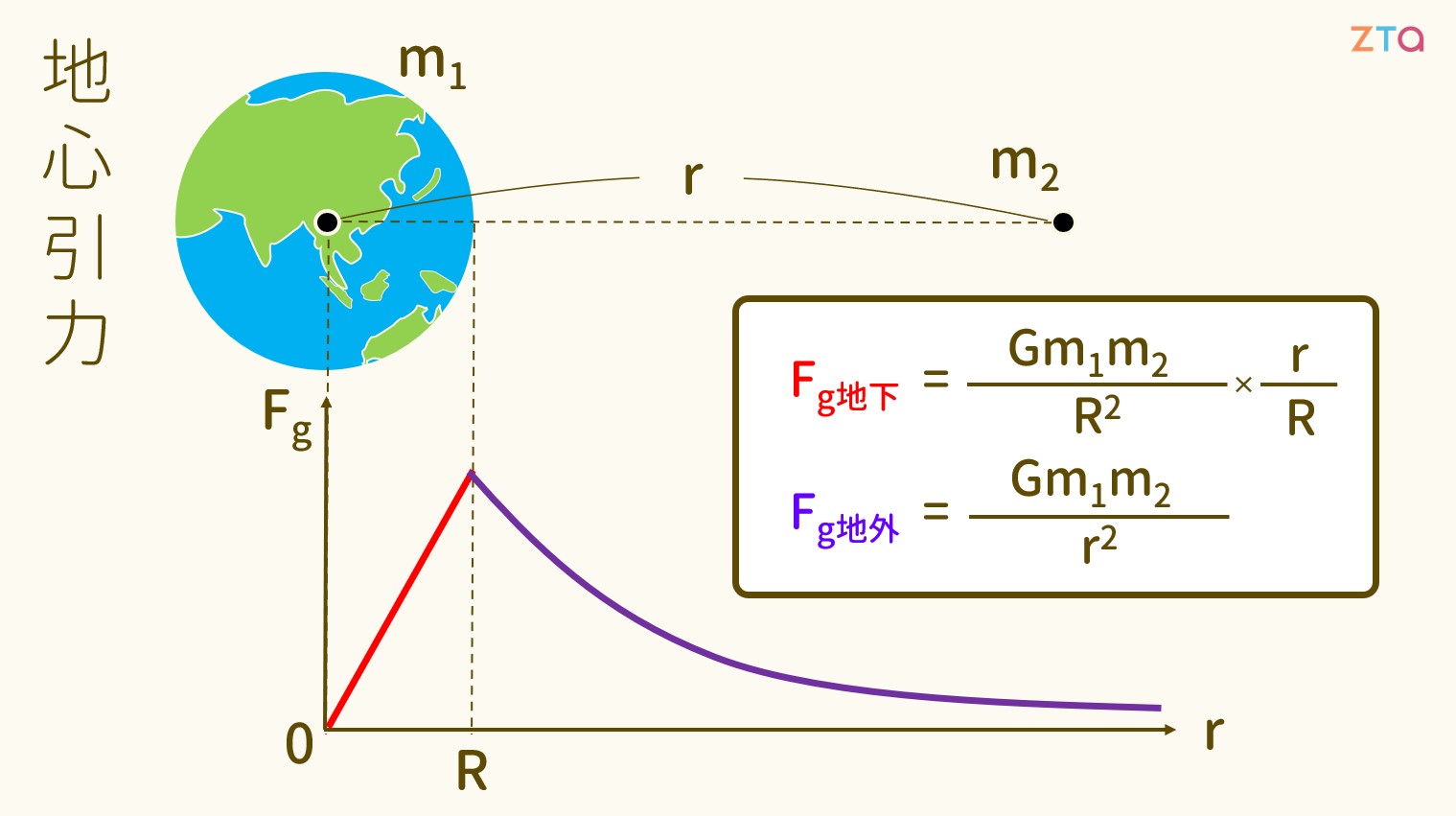
這裡需要注意的是,F_{g地下} 的式子只有在假設地球質量均勻分布的情形下才可以成立;然而實際上,地球的密度並非均勻。依照地球密度的不同,我們可以大致將地球由內而外分成內核、外核、地函、地殼四層,而這就屬於地球科學以及天文學的範疇了!